Цитата:
4)Очень простая, но правильное решение дают один-два из ста.
Имеем 100 кг ягод.
Влажность ягод (содержание воды в ягодах) - 99 %.
Ягоды полежали на солнце, подсохли. Влажность стала 98 %.
Вопрос. Сколько теперь ягоды весят?
В 100 кг ягод влажностью 99% 99 кг воды и 1 кг сухого вещества.
При влажности 98% 1 кг сухого в-ва это 2% от общей массы, значит 100% будет 50 кг.
Цитата:
5)Где подвох?
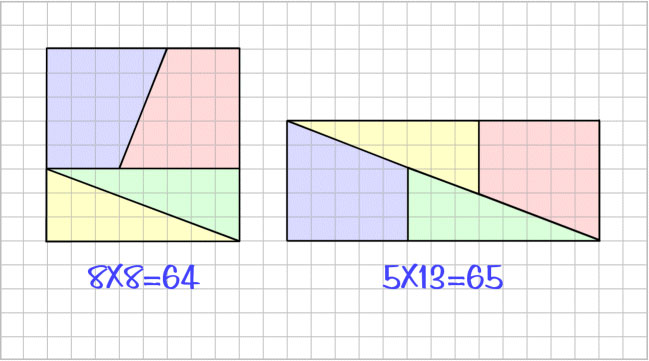
Все части первой фигуры точно не сложатся во вторую, внутри второй фигуры останется пустое место в виде вытянутого параллелограмма площадью 1 клетка.
Цитата:
10) В пруду плавает лодка. В лодке герасим с мумой.
Вопрос. Как изменится уровень воды в пруду если Герасим утопит в нем своё муму?
Расчеты не нужны. Ответить - увеличится, уменьшится или останется прежним и обосновать почему?
Допустим, для утопления муму к её шее привязан груз весом 1000 т и объёмом 1 кубометр. Плавая в лодке, этот груз вытесняет 1000 кубометров воды, а будучи выброшенным за борт -- всего 1 кубометр. Поэтому уровень в пруду уменьшится.
Цитата:
12.)Вот доказательство того, что 2=1:
1. 1=1
2. Одну единицу обозначаем за Х, вторую за У, получается Х=У;
3. Умножаем обе части тождества на Х, получаем Х2=ХУ;
4. Из обеих частей тождества отнимаем У2, получаем Х2 - У2=ХУ - У2;
5. Правую часть раскладывем как разность квадратов, а в левой выносим У за скобку, получаем: (Х-У)(Х+У)=У(Х-У);
6. Сокращаем обе части на (Х-У), получаем: Х+У=У
7. Подставим вместо Х и У единицы, получим: 1+1=1, т.е. 2=1.
Где здесь ошибка?
Х-У=0, поэтому при сокращении на (Х-У) получается деление на ноль...
Цитата:
13 )
Мудрецу задали вопрос:
- В деревне только один парикмахер, но он бреет тех, и только тех жителей своей деревни, которые не бреются сами, должен ли он брить самого себя?
Мудрец ответил:
- Если он себя не бреет, то он относится к тем жителям деревни, которых он должен брить. Значит, он должен себя брить. Если же он себя бреет, то он не относится к тем жителям своей своей деревни, которых он должен брить. Значит, он должен себя брить. Если же он себя бреет, то он не относится к тем жителям своей деревни, которых он должен брить. Значит, он не должен себя брить. Вот и весь ответ на ваш вопрос.
- Как же так, - продолжали спрашивать мудреца. - Если парикмахер себя не бреет, то он должен брить, а если он себя бреет, то не должен брить?
Так и есть, когда себя не бреет -- становится никем не бритый -- бреется, когда побрился -- не бреется, ибо нечего брить, ессно, пока опять не станет небритым. Никакого противоречия.

