Продолжаем решать задачи и отгадывать головоломки.
30) Задача про самолет (условие): Самолет (реактивный или винтовой) стоит на взлётной полосе с подвижным покрытием (типа транспортёра). Покрытие может двигаться против направления взлёта самолёта, то есть ему навстречу. Оно имеет систему управления, которая отслеживает и подстраивает скорость движения полотна таким образом, чтобы скорость вращения колёс самолёта была равна скорости движения полотна.
Вопрос: сможет ли самолёт разбежаться по этому полотну и взлететь?
Десяткин писал(а):
Естественно сможет. Если колеса не развалятся : , т.к. скорость их вращения будет в 2 раза выше, чем при обычном взлете. Ну учитывая это самолет будет чуть дольше разгоняться, теряя на потерях трения колес
31) Задача от vak Задача по электротехнике :Есть куб (грубо говоря из проволоки). У каждого ребра сопротивление 1 Ом. Какое будет общее сопротивление, если измерять на противоположных углах (вершинах)? Десяткин писал(а):
ну я представил схему так
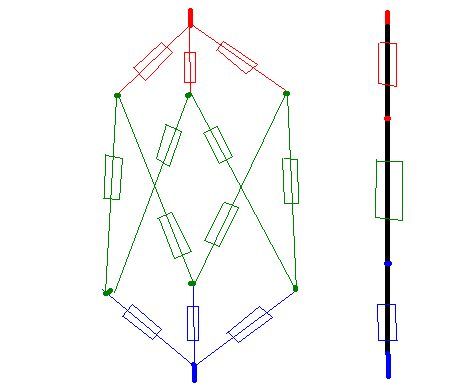
Схема абсолютно симметричная, по этому я позволил условно представить ее как три последовательно соединенных резистора. Для этого объединил в группы услолвнопараллельные резисторы. Т.е. соединил в точках. Ну ты понял в каких. Ибо токи везде одинаковые.
Если поменять сопротивление всех на любое другое значение, то ответ опять (по странным стечениям обстоятельств : ) совпадет с правильным.
1/3+1/6+1/3=5/6 32) Имеем последовательность.
5
15
1115
3115
132115
1113122115
и т.д.
Если начинать не с 5-ки а с единицы, возможно ли появление в n-ных членах последовательности цифр больше тройки?asokoloff писал(а):
возникнуть не может, достаточно рассуждать от обратного, т.е. предположить, что такая повторяемость существует.
например 311112, что описывает последовательность 11112, которой не может быть, поскольку содержит нечетное количество цифр, что невозможно.
например 2, 211112, описывает 1112, что правильно записать как 3112.
122223, 22233, 3213
и т.д.
четыре 1 выдают цикл, т.е. должны быть заданы изначально, чтобы появляться.
1111, описывают 1111, что должно быть задано как 41, а описывает те же 1111.
133332, описывает 3333222, что невозможно (2n-1)
3333, описывает 333333, что уже должно быть описано как 63.
невозможность причины, делает невозможным следствие.
33) asokoloff
На столе лежит 30 одинаковых монет, все орлом вверх.
Вам завязывают глаза, одевают перчатки и произвольно переворачивают 10 монет.
Затем предлагают разделить монеты на две кучки так, что бы в них было равное количество перевернутых решкой монет.
Как это сделать, если через перчатки вы не можете определить положение монет.Десяткин писал(а):
В одну кучку отобрать 10 монет. В другую соответственно 20 монет.
А затем все монеты в кучке, где их 10 штук перевернуть.
Как то так...
34) Один богач оставил завещание, в котором написал, что завещает всё своё богатство тому монастырю, который отслужит по нему количество обеден, равное половине количества дней, оставшихся существовать этому монастырю. Много монастырей хотело получить это богатство, но не знало, как выполнить условие завещания. Наконец, настоятель одного монастыря сказал, что он знает, как выполнить условие завещания. Как же он собирался выполнить его?HOMEr писал(а):
обедни служить через день.
35) На Луне все вещи весят в 6 раз меньше, чем на Земле.
Вообразите, что на Луне существует озеро с пресной водой. На озеро спущен пароход, который в земных пресноводных озёрах имеет осадку 3 метра. Как глубоко будет сидеть наш пароход в воде лунного озера?
Заодно решите и такую задачу: где не умеющий плавать человек может утонуть скорее - в земном озере или в нашем воображаемом лунном?36) Вы утром торопитесь на работу или в школу.
На столе стоит чашка горячего кофе, который вы должны выпить через пять минут.
Как лучше поступить, чтобы не обжечься:
сразу добавить холодное молоко, и пусть кофе постоит так;
добавить молоко в последний момент - перед тем, как выпить кофе,
разницы нет.asokoloff писал(а):
скорость термодинамического обмена тем выше, чем больше разница температур.
следовательно холодное молоко надо добавить в последний момент.
37) Полюсом холода на территории России считается якутское селение Оймякон, где зафиксированы температуры ниже 70 градусов мороза. А есть ли на Земле место, где ртутный столбик термометра показывает еще более низкую температуру, чем в России? Если есть, то где именно (только указать континент недостаточно).Сaptain писал(а):
Ртутный столбик термометра замерзает при -38,9С и показать температуру ниже -70С не в состоянии. Нет таких мест!
38 )
1.Есть 27 монет и весы.

2.Одна из них поддельная (фальшивая тяжелее).
3.Как за 3 взвешивания определить фальшивку?HOMEr писал(а):
А уж если известно, что фальшивка тяжелее, то всё просто!
Делим монеты на три равные кучки (по 9 монет).
1. Взвешиваем любые две.
При раВном весе дальнейшие манипуляции проводим с оставшейся кучкой и делим её на три кучки (по 3 монеты)
При раЗном весе делим на три кучки (по 3 монеты) более тяжёлую из двух взвешенных кучек.
2. Опять взвешиваем любые две.
При раВном весе дальнейшие манипуляции проводим с оставшейся кучкой и делим её на три (по 1 монете).
При раЗном весе делим на три (по 1 монете) более тяжёлую из двух взвешенных кучек.
3. Снова взвешиваем любые две монеты.
При раВном весе, фальшивка - оставшаяся монета.
При раЗном весе, фальшивка - более тяжёлая монета.
Если короче: делить монеты на три части и взвешивать любые две. Потом проделать то же самое с более тяжёлой частью.
39) Встретились два математика:
— Привет!
— Привет!
— Как дела?
— Хорошо. Растут три сына.
— А сколько им лет?
— Произведение их возрастов равно 36 а сумма их возрастов равна номеру этого дома.
— Этой информации мне не достаточно!
— Старший рыжий
— Вот теперь я знаю ответ на свой вопрос.
Назовите возраст сыновей.Сaptain писал(а):
Опять мне придётся!
Допустим, что нет сына с возрастом 1 год, тогда получим:
36=2*2*3*3
То есть 4*3*3, сумма 10,
либо 2*3*6, сумма 11,
либо 9*2*2, сумма 13.
Теперь допустим, что есть сын (сыновья) с возрастом 1 год, тогда двум оставшимся:
1 и 36, тогда сумма будет 1+1+36=38
2 и 18, тогда 1+2+18=21
3 и 12, тогда 1+3+12=16
4 и 9, тогда 1+4+9=14
6 и 6, тогда 1+6+6=13
Как видно, сумма 13 получается двумя способами, все остальные варианты дают однозначное решение.
И только уточнение, что есть сын, который старше двух остальных, проясняет дело.
Ответ: 9, 2 и 2.
40) 1.Есть 12 монет и весы.

2.Одна из них поддельная (фальшивая может быть тяжелее, а может и легче).
3.Как за 3 взвешивания определить фальшивку?asokoloff писал(а):
Маркируем монеты как Xn
Обозначаем "+", когда тяжелее
Обозначаем "-", когда легче
Обозначаем "N", когда это нормальная монета
Нумерованным списком обозначается ветвь рассуждения.
Взвешиваем X1-4 и X5-8, получаем:
1. X1-4+ X5-8- X9-12N
Рокируем монеты X1+ X5-. Взвешиваем монеты X2-5 и X1,9-11, получаем:
1.1. X2-5+ X1,9-11-
Делаем вывод, что X1,5 это монеты N; искомая монета +; это одна из монет X2-4
Взвешиваем монеты X2 и X3, получаем:
1.1.1. X2+ X3-
Искомая монета X2 и она тяжелее
1.1.2. X2- X3+
Искомая монета X3 и она тяжелее
1.1.3. X2N X3N
Искомая монета X4 и она тяжелее
1.2. X2-5- X1,9-11+
Делаем вывод, искомая монета X1 или X5
Взвешиваем X1 и X9, получаем:
1.2.1. X1+ X9-
Искомая монета X1 и она тяжелее
1.2.2. X1N X9N
Искомая монета X5 и она легче
1.3. X2-5N X1,9-11N
Делаем вывод, что искомая монета -; это одна из монет X6-8
Взвешиваем X6 и X7, получаем:
1.3.1. X6- X7+
Искомая монета X6 и она легче
1.3.2. X6+ X7-
Искомая монета X7 и она легче
1.3.3. X6N X7N
Искомая монета X8 и она легче
2. X1-8N X9-12?
Взвешиваем монеты X1-3 и X9-11, получаем:
2.1. X1-3+ X9-11-
Делаем вывод, что искомая монета -; это одна из монет X9-11
Взвешиваем X9 и X10, получаем:
2.1.1. X9- X10+
Искомая монета X9 и она легче
2.1.2. X9+ X10-
Искомая монета X10 и она легче
2.1.3. X9N X10N
Искомая монета X11 и она легче
2.2. X1-3- X9-11+
Делаем вывод, что искомая монета +; это одна из монет X9-11
Взвешиваем X9 и X10, получаем:
2.2.1. X9+ X10-
Искомая монета X9 и она тяжелее
2.2.2. X9- X10+
Искомая монета X10 и она тяжелее
2.2.3. X9N X10N
Искомая монета X11 и она тяжелее
2.3. X1-3N X9-11N
Делаем вывод, что искомая монета X12
Взвешиваем X1 и X12, получаем:
2.3.1. X1+ X12-
Искомая монета X12 и она легче
2.3.2. X1- X12+
Искомая монета X12 и она тяжелее
3. X1-4- X5-8+ X9-12N
Ветка и выводы отличаются от первой ветки только знаком
41) ARlll
как разместить 10 монет в 5 рядов(линий) по 4 шт?Десяткин писал(а):
Кладем монеты в месте пересечения (соединения) линий звезды

